Entropy
We can’t understand the second law until we know what entropy is. Mathematical formulas precisely define entropy, but hardly anyone can understand them without scientific training. A very well-guarded secret is that many people with scientific training, even those with doctorates in physics and chemistry, don’t understand entropy either. Here are a few points about the little-understood concept of entropy, all derived from physics.
Heat energy is disorganized energy. It can still do useful work if there is a machine, a structure, to take advantage of it. Automobile engines and living organisms are examples of heat engines. They take heat energy derived from fuel or food and can do useful work, while expelling low-temperature heat and degraded material. No heat engine is 100 percent efficient at converting heat energy into useful work. No matter how well engineers design the engine, it cannot be more efficient than a certain ideal machine that Nicolas Léonard Sadi Carnot (French physicist and military engineer, 1796–1832) described in 1824. His ideal machine, the Carnot engine, works with reversible cycles. “Reversible” means that a motor (or a person turning a crank) can drive a Carnot engine backwards and make the engine “undo” or reverse everything it does when running in the forward direction.
The efficiency of a Carnot engine depends only on the highest temperature H obtained by burning the fuel, and the lower temperature L of the environment. (The temperatures will never be negative numbers or zeros because we will always measure them in kelvins on the absolute temperature scale.) The number one (1) represents perfect, 100-percent efficiency. The efficiency of a reversible or Carnot engine is the number 1 less the fraction we obtain by dividing the lower temperature L by the highest temperature H. The fraction must always be a number less than one, because the numerator, the lower temperature, will always be smaller than the denominator, the highest temperature. This means that the Carnot efficiency must always be less than 1, and the efficiency of a real engine must be lower still.
We can’t understand the second law until we know what entropy is. Mathematical formulas precisely define entropy, but hardly anyone can understand them without scientific training. A very well-guarded secret is that many people with scientific training, even those with doctorates in physics and chemistry, don’t understand entropy either. Here are a few points about the little-understood concept of entropy, all derived from physics.
Heat energy is disorganized energy. It can still do useful work if there is a machine, a structure, to take advantage of it. Automobile engines and living organisms are examples of heat engines. They take heat energy derived from fuel or food and can do useful work, while expelling low-temperature heat and degraded material. No heat engine is 100 percent efficient at converting heat energy into useful work. No matter how well engineers design the engine, it cannot be more efficient than a certain ideal machine that Nicolas Léonard Sadi Carnot (French physicist and military engineer, 1796–1832) described in 1824. His ideal machine, the Carnot engine, works with reversible cycles. “Reversible” means that a motor (or a person turning a crank) can drive a Carnot engine backwards and make the engine “undo” or reverse everything it does when running in the forward direction.
The efficiency of a Carnot engine depends only on the highest temperature H obtained by burning the fuel, and the lower temperature L of the environment. (The temperatures will never be negative numbers or zeros because we will always measure them in kelvins on the absolute temperature scale.) The number one (1) represents perfect, 100-percent efficiency. The efficiency of a reversible or Carnot engine is the number 1 less the fraction we obtain by dividing the lower temperature L by the highest temperature H. The fraction must always be a number less than one, because the numerator, the lower temperature, will always be smaller than the denominator, the highest temperature. This means that the Carnot efficiency must always be less than 1, and the efficiency of a real engine must be lower still.
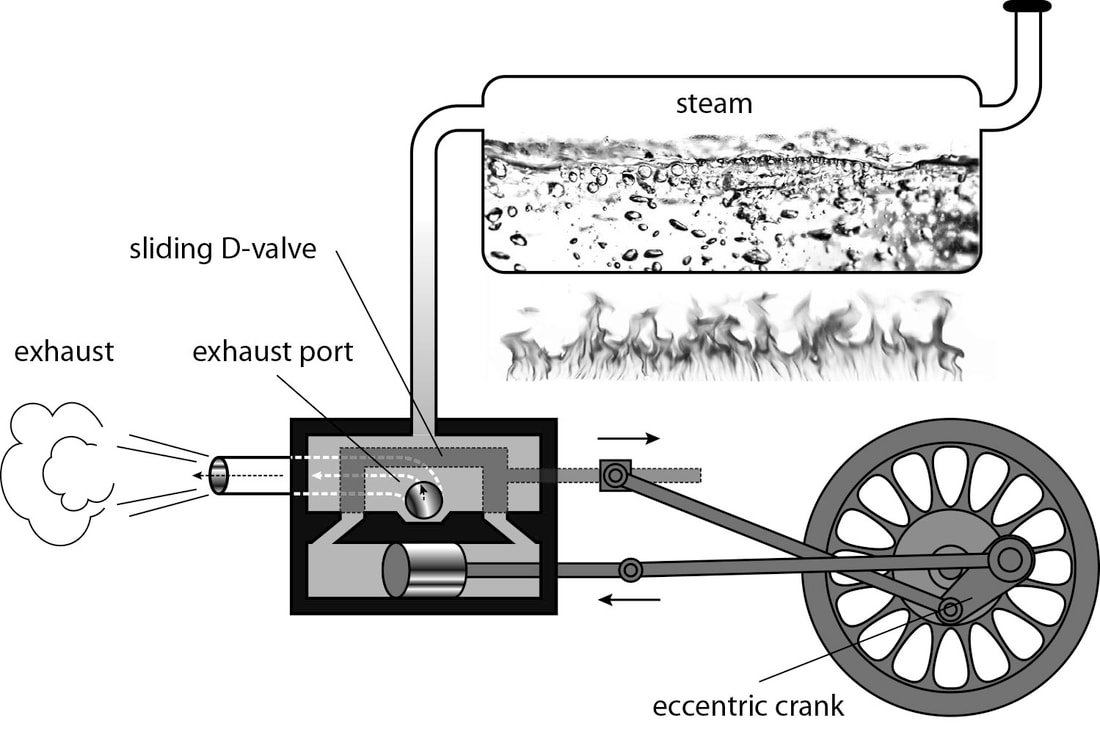
Now, how do we define entropy in this situation, without reference to the number of wrong arrangements of the steam molecules? Heat engines usually go through cycles. A quantity of steam at the high absolute temperature H enters a cylinder. The steam has a large quantity of heat energy Q. The steam works by pushing the moveable wall of the cylinder or piston back a certain distance, and a connecting rod communicates that motion to the flywheel. As the steam works it expands to fill the larger space it made. Expansion cools the steam to a lower absolute temperature L. When the steam has pushed the piston as far as the piston can go, that is the end of the power stroke but not the end of the cycle. At the end of the power stroke a mechanism attached to the engine opens an exhaust valve to let the cooled steam out. The inertia of the flywheel moves the piston back to its original position, driving the spent steam out of the cylinder. At this point the exhaust valve closes, the boiler valve opens to let in more hot steam, and the cycle repeats.
We calculate the entropy of the steam by adding up small changes as the steam passes from one state to another. Each small change is the quantity of heat the steam gains or loses divided by the steam’s temperature. At the beginning of the power stroke the quantity of heat Q is large, and the temperature H is high. That is, H is a large number. Dividing by a large number makes a small number, so steam at high temperature has low entropy. When the steam comes out of the cylinder at the end of the power stroke, its quantity q of heat is lower because some of the energy was extracted as useful work. At the same time the temperature L is low, that is, L is a small number. Dividing by a small number makes a large number, so steam at low temperature has high entropy. But we must remember that the quantity q of heat at the end of the power stroke is less than the quantity Q of heat at the beginning of the power stroke. The difference we get by subtracting q from Q is just the amount of useful work done in the cycle. The efficiency of the engine is the amount of useful work divided by the amount of heat energy it took to do that work, including the heat unavoidably wasted. That is, the efficiency is the quantity Q ‑ q divided by Q, which is equal to 1 less the ratio of q to Q. Comparing this formula with the formula for Carnot efficiency, we can see that the 1’s and the minus signs are the same. Therefore, if the real engine is as efficient as a Carnot engine, we will have the ratio of q to Q equal to the ratio of L to H. We can rearrange the ratios to find that the ratio of Q to H is equal to the ratio of q to L. Those two ratios are just the entropy of the steam before and after the power stroke. In a Carnot engine there is no increase in entropy because the two ratios are equal to each other. But in real engines with less than the best obtainable efficiency the amount of heat wasted must be greater than the minimum waste of the Carnot engine. That makes the ratio of q to Q for a real engine larger than the ratio of L to H. A real engine subtracts more from 1 than an ideal engine and has a lower efficiency. We can also rearrange the unequal ratios to find that the ratio of q to L is greater than the ratio of Q to H. This means that the entropy of the steam increases in each cycle of a real engine.
As an example, let’s subtract room temperature, about 300 kelvins, from the temperature of superheated steam, about 500 kelvins, to get the difference, 200 kelvins. Then we divide the difference by the higher temperature, 200 kelvins/500 kelvins = 2/5 = 40%, to get the efficiency. In so doing we have used the concept of entropy to show that no steam engine or coal-fired electric generator can be more than 40% efficient. We accept the wastefulness of heat engines because there is no way to make them better.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.
Feynman's Analysis
Richard Feynman (American physicist, 1918-1988) discussed a fan connected to a wheel with a ratchet and pawl that allowed it to turn only one way. Could such a device extract useful work from the thermal fluctuations of the air, if the fluctuations made air currents that turned the fan? After all, we do get useful work from windmills. Feynman analysed the difference between fluctuations driving a one-way fan and real windmills. He said:
Another delight of our subject of physics is that even simple and idealized things, like the ratchet and pawl, work only because they are part of the universe. The ratchet and pawl works in only one direction because it has some ultimate contact with the rest of the universe. If the ratchet and pawl were in a box and isolated for some sufficient time, the wheel would be no more likely to go one way than the other. But because we pull up the shades and let the light in, because we cool off the earth and get heat from the sun, the ratchets and pawls that we make can turn one way. This "one-wayness" is interrelated with the fact that the ratchet is part of the universe. It is part of the universe not only in the sense that it obeys the physical laws of the universe, but its one-way behavior is tied to the one-way behavior of the entire universe. It cannot be completely understood until the mystery of the beginnings of the history of the universe is reduced still further from speculation to scientific understanding.[i]
[i] Feynman, Richard P., Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Volume 1, (Reading, Massachusetts: Addison-Wesley, 1963), Section 46‑5, p. 46‑9.
The above quotation relates irreversibility to cosmic questions. Our quest clearly includes investigating such questions. Other related questions are as follows: What is the best way to do things? How far can we go designing useful things to make life easier? Why do things break down? Why is there decay and death? Are these processes reversible? Did life arise from random action? The process we would most like to be able to reverse is the process of dying. The second law has something important to say about these questions. Several of these concepts are related: entropy and information, disorder and design, decay and structure. Death and life are not necessarily related to the second law. We will discuss these far-reaching questions as we go along, but we must build up a number of other concepts first. Let’s start by saying that the second law of thermodynamics is intimately related to fundamental questions about “life, the universe, and everything.”Now, how do we define entropy in this situation, without reference to the number of wrong arrangements of the steam molecules? Heat engines usually go through cycles. A quantity of steam at the high absolute temperature H enters a cylinder. The steam has a large quantity of heat energy Q. The steam works by pushing the moveable wall of the cylinder or piston back a certain distance, and a connecting rod communicates that motion to the flywheel. As the steam works it expands to fill the larger space it made. Expansion cools the steam to a lower absolute temperature L. When the steam has pushed the piston as far as the piston can go, that is the end of the power stroke but not the end of the cycle. At the end of the power stroke a mechanism attached to the engine opens an exhaust valve to let the cooled steam out. The inertia of the flywheel moves the piston back to its original position, driving the spent steam out of the cylinder. At this point the exhaust valve closes, the boiler valve opens to let in more hot steam, and the cycle repeats.
We calculate the entropy of the steam by adding up small changes as the steam passes from one state to another. Each small change is the quantity of heat the steam gains or loses divided by the steam’s temperature. At the beginning of the power stroke the quantity of heat Q is large, and the temperature H is high. That is, H is a large number. Dividing by a large number makes a small number, so steam at high temperature has low entropy. When the steam comes out of the cylinder at the end of the power stroke, its quantity q of heat is lower because some of the energy was extracted as useful work. At the same time the temperature L is low, that is, L is a small number. Dividing by a small number makes a large number, so steam at low temperature has high entropy. But we must remember that the quantity q of heat at the end of the power stroke is less than the quantity Q of heat at the beginning of the power stroke. The difference we get by subtracting q from Q is just the amount of useful work done in the cycle. The efficiency of the engine is the amount of useful work divided by the amount of heat energy it took to do that work, including the heat unavoidably wasted. That is, the efficiency is the quantity Q ‑ q divided by Q, which is equal to 1 less the ratio of q to Q. Comparing this formula with the formula for Carnot efficiency, we can see that the 1’s and the minus signs are the same. Therefore, if the real engine is as efficient as a Carnot engine, we will have the ratio of q to Q equal to the ratio of L to H. We can rearrange the ratios to find that the ratio of Q to H is equal to the ratio of q to L. Those two ratios are just the entropy of the steam before and after the power stroke. In a Carnot engine there is no increase in entropy because the two ratios are equal to each other. But in real engines with less than the best obtainable efficiency the amount of heat wasted must be greater than the minimum waste of the Carnot engine. That makes the ratio of q to Q for a real engine larger than the ratio of L to H. A real engine subtracts more from 1 than an ideal engine and has a lower efficiency. We can also rearrange the unequal ratios to find that the ratio of q to L is greater than the ratio of Q to H. This means that the entropy of the steam increases in each cycle of a real engine.
As an example, let’s subtract room temperature, about 300 kelvins, from the temperature of superheated steam, about 500 kelvins, to get the difference, 200 kelvins. Then we divide the difference by the higher temperature, 200 kelvins/500 kelvins = 2/5 = 40%, to get the efficiency. In so doing we have used the concept of entropy to show that no steam engine or coal-fired electric generator can be more than 40% efficient. We accept the wastefulness of heat engines because there is no way to make them better.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.
We calculate the entropy of the steam by adding up small changes as the steam passes from one state to another. Each small change is the quantity of heat the steam gains or loses divided by the steam’s temperature. At the beginning of the power stroke the quantity of heat Q is large, and the temperature H is high. That is, H is a large number. Dividing by a large number makes a small number, so steam at high temperature has low entropy. When the steam comes out of the cylinder at the end of the power stroke, its quantity q of heat is lower because some of the energy was extracted as useful work. At the same time the temperature L is low, that is, L is a small number. Dividing by a small number makes a large number, so steam at low temperature has high entropy. But we must remember that the quantity q of heat at the end of the power stroke is less than the quantity Q of heat at the beginning of the power stroke. The difference we get by subtracting q from Q is just the amount of useful work done in the cycle. The efficiency of the engine is the amount of useful work divided by the amount of heat energy it took to do that work, including the heat unavoidably wasted. That is, the efficiency is the quantity Q ‑ q divided by Q, which is equal to 1 less the ratio of q to Q. Comparing this formula with the formula for Carnot efficiency, we can see that the 1’s and the minus signs are the same. Therefore, if the real engine is as efficient as a Carnot engine, we will have the ratio of q to Q equal to the ratio of L to H. We can rearrange the ratios to find that the ratio of Q to H is equal to the ratio of q to L. Those two ratios are just the entropy of the steam before and after the power stroke. In a Carnot engine there is no increase in entropy because the two ratios are equal to each other. But in real engines with less than the best obtainable efficiency the amount of heat wasted must be greater than the minimum waste of the Carnot engine. That makes the ratio of q to Q for a real engine larger than the ratio of L to H. A real engine subtracts more from 1 than an ideal engine and has a lower efficiency. We can also rearrange the unequal ratios to find that the ratio of q to L is greater than the ratio of Q to H. This means that the entropy of the steam increases in each cycle of a real engine.
As an example, let’s subtract room temperature, about 300 kelvins, from the temperature of superheated steam, about 500 kelvins, to get the difference, 200 kelvins. Then we divide the difference by the higher temperature, 200 kelvins/500 kelvins = 2/5 = 40%, to get the efficiency. In so doing we have used the concept of entropy to show that no steam engine or coal-fired electric generator can be more than 40% efficient. We accept the wastefulness of heat engines because there is no way to make them better.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.
Feynman's Analysis
Richard Feynman (American physicist, 1918-1988) discussed a fan connected to a wheel with a ratchet and pawl that allowed it to turn only one way. Could such a device extract useful work from the thermal fluctuations of the air, if the fluctuations made air currents that turned the fan? After all, we do get useful work from windmills. Feynman analysed the difference between fluctuations driving a one-way fan and real windmills. He said:
Another delight of our subject of physics is that even simple and idealized things, like the ratchet and pawl, work only because they are part of the universe. The ratchet and pawl works in only one direction because it has some ultimate contact with the rest of the universe. If the ratchet and pawl were in a box and isolated for some sufficient time, the wheel would be no more likely to go one way than the other. But because we pull up the shades and let the light in, because we cool off the earth and get heat from the sun, the ratchets and pawls that we make can turn one way. This "one-wayness" is interrelated with the fact that the ratchet is part of the universe. It is part of the universe not only in the sense that it obeys the physical laws of the universe, but its one-way behavior is tied to the one-way behavior of the entire universe. It cannot be completely understood until the mystery of the beginnings of the history of the universe is reduced still further from speculation to scientific understanding.[i]
[i] Feynman, Richard P., Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Volume 1, (Reading, Massachusetts: Addison-Wesley, 1963), Section 46‑5, p. 46‑9.
The above quotation relates irreversibility to cosmic questions. Our quest clearly includes investigating such questions. Other related questions are as follows: What is the best way to do things? How far can we go designing useful things to make life easier? Why do things break down? Why is there decay and death? Are these processes reversible? Did life arise from random action? The process we would most like to be able to reverse is the process of dying. The second law has something important to say about these questions. Several of these concepts are related: entropy and information, disorder and design, decay and structure. Death and life are not necessarily related to the second law. We will discuss these far-reaching questions as we go along, but we must build up a number of other concepts first. Let’s start by saying that the second law of thermodynamics is intimately related to fundamental questions about “life, the universe, and everything.”Now, how do we define entropy in this situation, without reference to the number of wrong arrangements of the steam molecules? Heat engines usually go through cycles. A quantity of steam at the high absolute temperature H enters a cylinder. The steam has a large quantity of heat energy Q. The steam works by pushing the moveable wall of the cylinder or piston back a certain distance, and a connecting rod communicates that motion to the flywheel. As the steam works it expands to fill the larger space it made. Expansion cools the steam to a lower absolute temperature L. When the steam has pushed the piston as far as the piston can go, that is the end of the power stroke but not the end of the cycle. At the end of the power stroke a mechanism attached to the engine opens an exhaust valve to let the cooled steam out. The inertia of the flywheel moves the piston back to its original position, driving the spent steam out of the cylinder. At this point the exhaust valve closes, the boiler valve opens to let in more hot steam, and the cycle repeats.
We calculate the entropy of the steam by adding up small changes as the steam passes from one state to another. Each small change is the quantity of heat the steam gains or loses divided by the steam’s temperature. At the beginning of the power stroke the quantity of heat Q is large, and the temperature H is high. That is, H is a large number. Dividing by a large number makes a small number, so steam at high temperature has low entropy. When the steam comes out of the cylinder at the end of the power stroke, its quantity q of heat is lower because some of the energy was extracted as useful work. At the same time the temperature L is low, that is, L is a small number. Dividing by a small number makes a large number, so steam at low temperature has high entropy. But we must remember that the quantity q of heat at the end of the power stroke is less than the quantity Q of heat at the beginning of the power stroke. The difference we get by subtracting q from Q is just the amount of useful work done in the cycle. The efficiency of the engine is the amount of useful work divided by the amount of heat energy it took to do that work, including the heat unavoidably wasted. That is, the efficiency is the quantity Q ‑ q divided by Q, which is equal to 1 less the ratio of q to Q. Comparing this formula with the formula for Carnot efficiency, we can see that the 1’s and the minus signs are the same. Therefore, if the real engine is as efficient as a Carnot engine, we will have the ratio of q to Q equal to the ratio of L to H. We can rearrange the ratios to find that the ratio of Q to H is equal to the ratio of q to L. Those two ratios are just the entropy of the steam before and after the power stroke. In a Carnot engine there is no increase in entropy because the two ratios are equal to each other. But in real engines with less than the best obtainable efficiency the amount of heat wasted must be greater than the minimum waste of the Carnot engine. That makes the ratio of q to Q for a real engine larger than the ratio of L to H. A real engine subtracts more from 1 than an ideal engine and has a lower efficiency. We can also rearrange the unequal ratios to find that the ratio of q to L is greater than the ratio of Q to H. This means that the entropy of the steam increases in each cycle of a real engine.
As an example, let’s subtract room temperature, about 300 kelvins, from the temperature of superheated steam, about 500 kelvins, to get the difference, 200 kelvins. Then we divide the difference by the higher temperature, 200 kelvins/500 kelvins = 2/5 = 40%, to get the efficiency. In so doing we have used the concept of entropy to show that no steam engine or coal-fired electric generator can be more than 40% efficient. We accept the wastefulness of heat engines because there is no way to make them better.
A Carnot engine is as efficient as possible. It has no increase in entropy and is therefore reversible. Since the engine is reversible, we can take a second Carnot engine identical to the first and run it backwards, driving it with the first engine. A reversed Carnot engine is an ideal refrigerator. It can take all the waste steam from the first engine, raise it to a high temperature, and discharge it in the boiler of the first engine. The combination of the two engines is equivalent to no heat flow at all. The second law of thermodynamics connects ideal processes with the concept of reversibility. Real heat engines are imperfect and irreversible, that is, their processes cause an increase in entropy. This relates some irreversible processes with the laws of physics.