Entropía
No podemos entender la segunda ley hasta que sepamos qué es la entropía. Las fórmulas matemáticas definen con precisión la entropía, pero casi nadie puede entenderlas sin formación científica. Un secreto muy bien guardado es que muchas personas con formación científica, incluso doctorados en física y química, tampoco entienden la entropía. Aquí hay algunos puntos sobre el concepto poco entendido de entropía, todos derivados de la física.
La energía térmica es energía desorganizada. Todavía puede hacer un trabajo útil si hay una máquina, una estructura, para aprovecharlo. Los motores de automóviles y los organismos vivos son ejemplos de motores térmicos. Toman la energía térmica derivada del combustible o los alimentos y pueden realizar trabajo útil, mientras expulsan calor a baja temperatura y materia degradado. Ningún motor térmico es 100 por ciento eficiente en la conversión de energía térmica a trabajo útil. No importa lo bien que los ingenieros diseñen el motor; no puede ser más eficiente que cierta máquina ideal que Nicolas Léonard Sadi Carnot (físico e ingeniero militar francés, 1796–1832) describió en 1824. Su máquina ideal, el motor de Carnot, funciona con ciclos reversibles. "Reversible" significa que un motor (o una persona que gira una manivela) puede hacer retroceder un motor de Carnot y hacer que el motor "deshaga" o invierta todo lo que hace cuando funciona hacia adelante.
La eficiencia de una máquina de Carnot depende únicamente de la temperatura más alta A obtenida al quemar el combustible y la temperatura más baja B del ambiente. (Las temperaturas nunca serán números negativos o ceros porque siempre las mediremos en grados Kelvin en la escala de temperatura absoluta). El número uno (1) representa una eficiencia perfecta del 100 por ciento. La eficiencia de un motor reversible o de Carnot es el número 1 menos la fracción que obtenemos al dividir la temperatura más baja B por la temperatura más alta A. La fracción siempre debe ser un número menor que uno, porque el numerador, la temperatura más baja, siempre será ser menor que el denominador, la temperatura más alta. Esto significa que la eficiencia de Carnot siempre debe ser menor que 100 por ciento, y la eficiencia de un motor real debe ser aún menor.
No podemos entender la segunda ley hasta que sepamos qué es la entropía. Las fórmulas matemáticas definen con precisión la entropía, pero casi nadie puede entenderlas sin formación científica. Un secreto muy bien guardado es que muchas personas con formación científica, incluso doctorados en física y química, tampoco entienden la entropía. Aquí hay algunos puntos sobre el concepto poco entendido de entropía, todos derivados de la física.
La energía térmica es energía desorganizada. Todavía puede hacer un trabajo útil si hay una máquina, una estructura, para aprovecharlo. Los motores de automóviles y los organismos vivos son ejemplos de motores térmicos. Toman la energía térmica derivada del combustible o los alimentos y pueden realizar trabajo útil, mientras expulsan calor a baja temperatura y materia degradado. Ningún motor térmico es 100 por ciento eficiente en la conversión de energía térmica a trabajo útil. No importa lo bien que los ingenieros diseñen el motor; no puede ser más eficiente que cierta máquina ideal que Nicolas Léonard Sadi Carnot (físico e ingeniero militar francés, 1796–1832) describió en 1824. Su máquina ideal, el motor de Carnot, funciona con ciclos reversibles. "Reversible" significa que un motor (o una persona que gira una manivela) puede hacer retroceder un motor de Carnot y hacer que el motor "deshaga" o invierta todo lo que hace cuando funciona hacia adelante.
La eficiencia de una máquina de Carnot depende únicamente de la temperatura más alta A obtenida al quemar el combustible y la temperatura más baja B del ambiente. (Las temperaturas nunca serán números negativos o ceros porque siempre las mediremos en grados Kelvin en la escala de temperatura absoluta). El número uno (1) representa una eficiencia perfecta del 100 por ciento. La eficiencia de un motor reversible o de Carnot es el número 1 menos la fracción que obtenemos al dividir la temperatura más baja B por la temperatura más alta A. La fracción siempre debe ser un número menor que uno, porque el numerador, la temperatura más baja, siempre será ser menor que el denominador, la temperatura más alta. Esto significa que la eficiencia de Carnot siempre debe ser menor que 100 por ciento, y la eficiencia de un motor real debe ser aún menor.
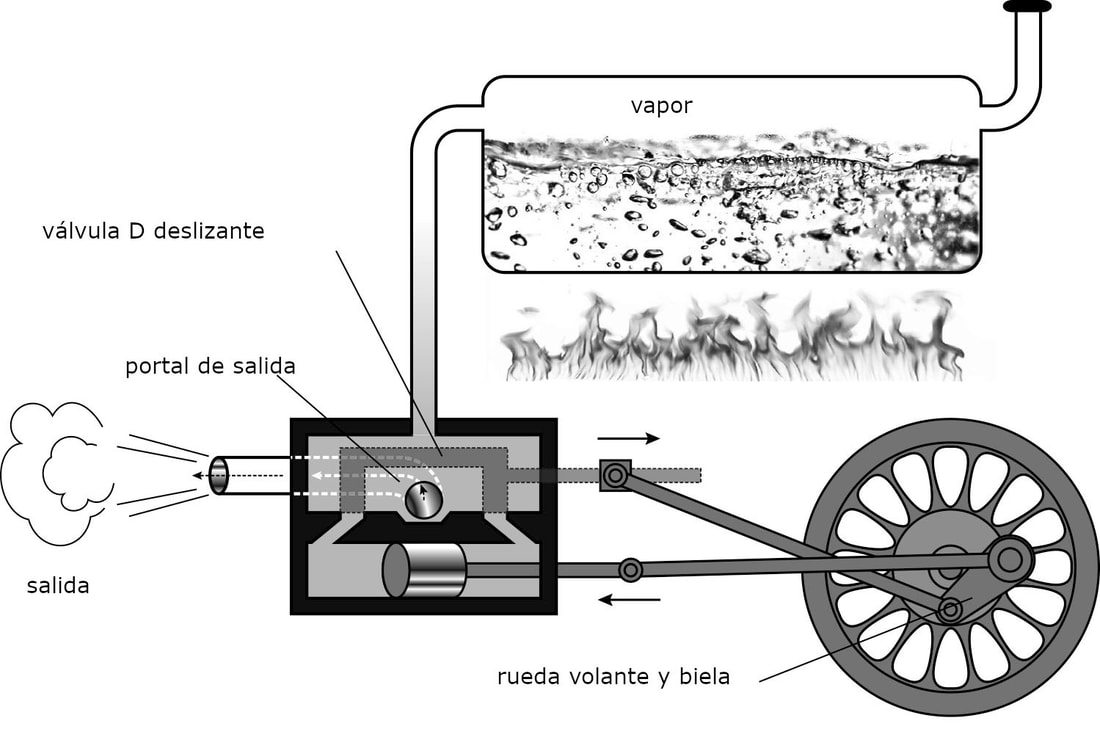
Ahora bien, ¿cómo definimos la entropía en esta situación, sin hacer referencia al número de arreglos aleatorios de las moléculas de vapor? Los motores térmicos suelen pasar por ciclos. Una cantidad de vapor a la alta temperatura absoluta A entra en un cilindro. El vapor tiene una gran cantidad de energía térmica Q. El vapor funciona empujando la pared móvil del cilindro o pistón hacia atrás una cierta distancia, y una biela comunica ese movimiento a la rueda volante. A medida que el vapor funciona, se expande para llenar el espacio más grande que hizo al empujar el pistón. La expansión enfría el vapor a una temperatura absoluta más baja B. Cuando el vapor ha empujado el pistón hasta donde puede llegar, ese es el final de la parte del ciclo que produce potencia, pero no el final del ciclo. Al final parte del ciclo que produce potencia, un mecanismo adjunto al motor abre una válvula de escape para dejar salir el vapor enfriado. La inercia de la rueda volante mueve el pistón de regreso a su posición original, expulsando el vapor gastado fuera del cilindro. En este punto, la válvula de escape se cierra, la válvula de la caldera se abre para dejar entrar más vapor caliente, y el ciclo se repite.
Calculamos la entropía del vapor sumando pequeños cambios a medida que el vapor pasa de un estado a otro. Cada pequeño cambio es la cantidad de calor que gana o pierde el vapor, dividida por la temperatura del vapor. Al comienzo de la parte del ciclo que produce potencia, la cantidad de calor Q es grande y la temperatura A es alta. Es decir, A es un número grande. Dividir por un número grande da como resultado un número pequeño, por lo que el vapor a alta temperatura tiene una entropía baja. Cuando el vapor sale del cilindro al final del parte del ciclo que produce potencia, su cantidad q de calor es menor porque parte de la energía se extrajo como trabajo útil. Al mismo tiempo, la temperatura B es baja, es decir, B es un número pequeño. Dividir por un número pequeño da como resultado un número grande, por lo que el vapor a baja temperatura tiene una entropía alta. Pero debemos recordar que la cantidad q de calor al final de la carrera de potencia es menor que la cantidad Q de calor al comienzo de la carrera de potencia. La diferencia que obtenemos al restar q de Q es solo la cantidad de trabajo útil realizado en el ciclo. La eficiencia del motor es la cantidad de trabajo útil dividida por la cantidad de energía térmica necesaria para realizar ese trabajo, incluyendo el calor inevitablemente desperdiciado. Es decir, la eficiencia es la cantidad Q - q dividida por Q, que es igual a 1 menos la razón de q a Q. Comparando esta fórmula con la fórmula de la eficiencia de Carnot, podemos ver que los unos y los signos menos son iguales. Por lo tanto, si la máquina real es tan eficiente como una máquina de Carnot, tendremos la razón de q a Q igual a la razón de B a A. Podemos reordenar las razones para encontrar que la razón de Q a A es igual a la razón de q a B. Esas dos razones son solo la entropía del vapor antes y después del parte del ciclo que produce potencia. En una máquina de Carnot no hay aumento de entropía porque las dos razones son iguales. Pero en los motores reales con menos de la mejor eficiencia obtenible, la cantidad de calor desperdiciado debe ser mayor que el desperdicio mínimo del motor de Carnot. Eso hace que la razón de q a Q para un motor real sea mayor que la razón de B a A. Un motor real resta más de 1 que un motor ideal y tiene una eficiencia más baja. También podemos reorganizar las razones desiguales para encontrar que la razón de q a B es mayor que la razón de Q a A. Esto significa que la entropía del vapor aumenta en cada ciclo de un motor real.
Como ejemplo, restemos la temperatura ambiente, unos 300 kelvin, de la temperatura del vapor sobrecalentado, unos 500 kelvin, para obtener la diferencia, 200 kelvin. Luego dividimos la diferencia por la temperatura más alta, 200 kelvin/500 kelvin = 2/5 = 40 %, para obtener la eficiencia. Al hacerlo, hemos utilizado el concepto de entropía para mostrar que ninguna máquina de vapor o generador eléctrico de combustible de carbón puede tener una eficiencia superior al 40%. Aceptamos el despilfarro de los motores térmicos porque no hay forma de mejorarlos.
Una máquina de Carnot es lo más eficiente posible. No tiene aumento de entropía y, por lo tanto, es reversible. Dado que el motor es reversible, podemos tomar un segundo motor de Carnot idéntico al primero y hacerlo funcionar al reverse, impulsándolo con el primer motor. Un motor de Carnot funcionando al reverse es un refrigerador ideal. Puede tomar todo el vapor residual del primer motor, elevarlo a alta temperatura y descargarlo en la caldera del primer motor. La combinación de los dos motores es equivalente a ningún flujo de calor. La segunda ley de la termodinámica conecta los procesos ideales con el concepto de reversibilidad. Los motores térmicos reales son imperfectos e irreversibles, es decir, sus procesos provocan un aumento de la entropía. Esto relaciona algunos procesos irreversibles con las leyes de la física.
El análisis de Feynman
Richard Feynman (físico estadounidense, 1918-1988) habló sobre un ventilador conectado a una rueda dentada y un trinquete que le permitía girar en una sola dirección. ¿Podría tal dispositivo extraer un trabajo útil de las fluctuaciones térmicas del aire, si las fluctuaciones generaran corrientes de aire que hicieran girar el ventilador? Después de todo, obtenemos trabajo útil de los molinos de viento. Feynman analizó la diferencia entre las fluctuaciones que impulsan un ventilador unidireccional y los molinos de viento reales. Él dijo:
“Otro aspecto de nuestro tema de la física es que incluso las cosas simples e idealizadas, como la rueda dentada y el trinquete, funcionan solo porque son parte del universo. La rueda dentada y el trinquete funcionan en una sola dirección porque tienen algún contacto final con el resto del universo. Si la rueda dentada y el trinquete estuvieran en una caja y aislados durante un tiempo suficiente, no sería más probable que la rueda se moviera en un sentido que en el otro. Pero debido a que levantamos las persianas y dejamos entrar la luz, porque refrescamos el medio ambiente y recibimos el calor del sol, la rueda dentada y el trinquete que fabricamos pueden girar en una dirección. Esta "unidireccionalidad" está interrelacionada con el hecho de que la rueda dentada y el trinquete son partes del universo. Son partes del universo no solo en el sentido de que obedecen las leyes físicas del universo, sino que su comportamiento unidireccional está ligado al comportamiento unidireccional de todo el universo. No puede entenderse eso completamente hasta que el misterio de los comienzos de la historia del universo se reduzca aún más de la especulación a la comprensión científica.”[i]
[i] Feynman, Richard P., Robert B. Leighton y Matthew Sands, The Feynman Lectures on Physics [Las lecciones de Feynman sobre la física], volumen 1, (Reading, Massachusetts: Addison-Wesley, 1963), sección 46 5, p. 46 9.
La cita anterior relaciona la irreversibilidad con cuestiones cósmicas. Nuestra búsqueda incluye claramente investigar tales cuestiones.
Otras preguntas relacionadas son las siguientes: ¿Cuál es la mejor manera de hacer las cosas? ¿Hasta dónde podemos llegar diseñando cosas útiles para hacer la vida más fácil? ¿Por qué las cosas se rompen? ¿Por qué hay decadencia y muerte? ¿Son estos procesos reversibles? ¿Surgió la vida de una acción aleatoria?
El proceso que más nos gustaría poder revertir es el proceso de morir.
La segunda ley tiene algo importante que decir acerca de estas cuestiones. Varios de estos conceptos están relacionados: entropía e información, desorden y diseño, decadencia y estructura. La muerte y la vida no están necesariamente relacionadas con la segunda ley.
Discutiremos estas preguntas de gran alcance a medida que avanzamos, pero primero debemos construir una serie de otros conceptos. Comenzamos diciendo que la segunda ley de la termodinámica está íntimamente relacionada con cuestiones fundamentales sobre “la vida, el universo y todo.” Ahora bien, ¿cómo definimos la entropía en esta situación, sin hacer referencia al número de arreglos aleatorios de las moléculas de vapor? Los motores térmicos suelen pasar por ciclos. Una cantidad de vapor a la alta temperatura absoluta A entra en un cilindro. El vapor tiene una gran cantidad de energía térmica Q. El vapor funciona empujando la pared móvil del cilindro o pistón hacia atrás una cierta distancia, y una biela comunica ese movimiento al volante. A medida que el vapor funciona, se expande para llenar el espacio más grande que hizo. La expansión enfría el vapor a una temperatura absoluta más baja L. Cuando el vapor ha empujado el pistón hasta donde puede llegar, ese es el final de la parte del ciclo que produce potencia, pero no el final del ciclo. Al final de la parte del ciclo que produce potencia, un mecanismo adjunto al motor abre una válvula de escape para dejar salir el vapor enfriado. La inercia de la rueda volante mueve el pistón de regreso a su posición original, expulsando el vapor gastado fuera del cilindro. En este punto, la válvula de escape se cierra, la válvula de la caldera se abre para dejar entrar más vapor caliente y el ciclo se repite.
Calculamos la entropía del vapor sumando pequeños cambios a medida que el vapor pasa de un estado a otro. Cada pequeño cambio es la cantidad de calor que gana o pierde el vapor, dividida por la temperatura del vapor. Al comienzo de la parte del ciclo que produce potencia, la cantidad de calor Q es grande y la temperatura A es alta. Es decir, A es un número grande. Dividir por un número grande da como resultado un número pequeño, por lo que el vapor a alta temperatura tiene una entropía baja. Cuando el vapor sale del cilindro al final del parte del ciclo que produce potencia, su cantidad q de calor es menor porque parte de la energía se extrajo como trabajo útil. Al mismo tiempo, la temperatura B es baja, es decir, B es un número pequeño. Dividir por un número pequeño da como resultado un número grande, por lo que el vapor a baja temperatura tiene una entropía alta. Pero debemos recordar que la cantidad q de calor al final de la carrera de potencia es menor que la cantidad Q de calor al comienzo de la carrera de potencia. La diferencia que obtenemos al restar q de Q es solo la cantidad de trabajo útil realizado en el ciclo. La eficiencia del motor es la cantidad de trabajo útil dividida por la cantidad de energía térmica necesaria para realizar ese trabajo, incluyendo el calor inevitablemente desperdiciado. Es decir, la eficiencia es la cantidad Q - q dividida por Q, que es igual a 1 menos la razón de q a Q. Comparando esta fórmula con la fórmula de la eficiencia de Carnot, podemos ver que los unos y los signos menos son iguales. Por lo tanto, si la máquina real es tan eficiente como una máquina de Carnot, tendremos la razón de q a Q igual a la razón de B a A. Podemos reordenar las razones para encontrar que la razón de Q a A es igual a la razón de q a B. Esas dos razones son solo la entropía del vapor antes y después del parte del ciclo que produce potencia. En una máquina de Carnot no hay aumento de entropía porque las dos razones son iguales. Pero en los motores reales con menos de la mejor eficiencia obtenible, la cantidad de calor desperdiciado debe ser mayor que el desperdicio mínimo del motor de Carnot. Eso hace que la razón de q a Q para un motor real sea mayor que la razón de B a A. Un motor real resta más de 1 que un motor ideal y tiene una eficiencia más baja. También podemos reorganizar las razones desiguales para encontrar que la razón de q a B es mayor que la razón de Q a A. Esto significa que la entropía del vapor aumenta en cada ciclo de un motor real.
Como ejemplo, restemos la temperatura ambiente, unos 300 kelvin, de la temperatura del vapor sobrecalentado, unos 500 kelvin, para obtener la diferencia, 200 kelvin. Luego dividimos la diferencia por la temperatura más alta, 200 kelvin/500 kelvin = 2/5 = 40 %, para obtener la eficiencia. Al hacerlo, hemos utilizado el concepto de entropía para mostrar que ninguna máquina de vapor o generador eléctrico de combustible de carbón puede tener una eficiencia superior al 40%. Aceptamos el despilfarro de los motores térmicos porque no hay forma de mejorarlos.
Una máquina de Carnot es lo más eficiente posible. No tiene aumento de entropía y, por lo tanto, es reversible. Dado que el motor es reversible, podemos tomar un segundo motor de Carnot idéntico al primero y hacerlo funcionar al reverse, impulsándolo con el primer motor. Un motor de Carnot funcionando al reverse es un refrigerador ideal. Puede tomar todo el vapor residual del primer motor, elevarlo a alta temperatura y descargarlo en la caldera del primer motor. La combinación de los dos motores es equivalente a ningún flujo de calor. La segunda ley de la termodinámica conecta los procesos ideales con el concepto de reversibilidad. Los motores térmicos reales son imperfectos e irreversibles, es decir, sus procesos provocan un aumento de la entropía. Esto relaciona algunos procesos irreversibles con las leyes de la física.
El análisis de Feynman
Richard Feynman (físico estadounidense, 1918-1988) habló sobre un ventilador conectado a una rueda dentada y un trinquete que le permitía girar en una sola dirección. ¿Podría tal dispositivo extraer un trabajo útil de las fluctuaciones térmicas del aire, si las fluctuaciones generaran corrientes de aire que hicieran girar el ventilador? Después de todo, obtenemos trabajo útil de los molinos de viento. Feynman analizó la diferencia entre las fluctuaciones que impulsan un ventilador unidireccional y los molinos de viento reales. Él dijo:
“Otro aspecto de nuestro tema de la física es que incluso las cosas simples e idealizadas, como la rueda dentada y el trinquete, funcionan solo porque son parte del universo. La rueda dentada y el trinquete funcionan en una sola dirección porque tienen algún contacto final con el resto del universo. Si la rueda dentada y el trinquete estuvieran en una caja y aislados durante un tiempo suficiente, no sería más probable que la rueda se moviera en un sentido que en el otro. Pero debido a que levantamos las persianas y dejamos entrar la luz, porque refrescamos el medio ambiente y recibimos el calor del sol, la rueda dentada y el trinquete que fabricamos pueden girar en una dirección. Esta "unidireccionalidad" está interrelacionada con el hecho de que la rueda dentada y el trinquete son partes del universo. Son partes del universo no solo en el sentido de que obedecen las leyes físicas del universo, sino que su comportamiento unidireccional está ligado al comportamiento unidireccional de todo el universo. No puede entenderse eso completamente hasta que el misterio de los comienzos de la historia del universo se reduzca aún más de la especulación a la comprensión científica.”[i]
[i] Feynman, Richard P., Robert B. Leighton y Matthew Sands, The Feynman Lectures on Physics [Las lecciones de Feynman sobre la física], volumen 1, (Reading, Massachusetts: Addison-Wesley, 1963), sección 46 5, p. 46 9.
La cita anterior relaciona la irreversibilidad con cuestiones cósmicas. Nuestra búsqueda incluye claramente investigar tales cuestiones.
Otras preguntas relacionadas son las siguientes: ¿Cuál es la mejor manera de hacer las cosas? ¿Hasta dónde podemos llegar diseñando cosas útiles para hacer la vida más fácil? ¿Por qué las cosas se rompen? ¿Por qué hay decadencia y muerte? ¿Son estos procesos reversibles? ¿Surgió la vida de una acción aleatoria?
El proceso que más nos gustaría poder revertir es el proceso de morir.
La segunda ley tiene algo importante que decir acerca de estas cuestiones. Varios de estos conceptos están relacionados: entropía e información, desorden y diseño, decadencia y estructura. La muerte y la vida no están necesariamente relacionadas con la segunda ley.
Discutiremos estas preguntas de gran alcance a medida que avanzamos, pero primero debemos construir una serie de otros conceptos. Comenzamos diciendo que la segunda ley de la termodinámica está íntimamente relacionada con cuestiones fundamentales sobre “la vida, el universo y todo.” Ahora bien, ¿cómo definimos la entropía en esta situación, sin hacer referencia al número de arreglos aleatorios de las moléculas de vapor? Los motores térmicos suelen pasar por ciclos. Una cantidad de vapor a la alta temperatura absoluta A entra en un cilindro. El vapor tiene una gran cantidad de energía térmica Q. El vapor funciona empujando la pared móvil del cilindro o pistón hacia atrás una cierta distancia, y una biela comunica ese movimiento al volante. A medida que el vapor funciona, se expande para llenar el espacio más grande que hizo. La expansión enfría el vapor a una temperatura absoluta más baja L. Cuando el vapor ha empujado el pistón hasta donde puede llegar, ese es el final de la parte del ciclo que produce potencia, pero no el final del ciclo. Al final de la parte del ciclo que produce potencia, un mecanismo adjunto al motor abre una válvula de escape para dejar salir el vapor enfriado. La inercia de la rueda volante mueve el pistón de regreso a su posición original, expulsando el vapor gastado fuera del cilindro. En este punto, la válvula de escape se cierra, la válvula de la caldera se abre para dejar entrar más vapor caliente y el ciclo se repite.